Los “cuatro de Trinity”, como en ocasiones se les llamaba, empezaron a compartir problemas matemáticos e intentar resolverlos. Uno de los primeros en los que empezaron a trabajar fue la “cuadratura del cuadrado”
Los ‘Cuatro de Trinity’ comprobaron que sí existen cuadrados que se pueden dividir en cuadrados más pequeños, todos ellos de distinto tamaño.
Éranse una vez cuatro estudiantes del Trinity College en Cambridge (Reino Unido), centro que se considera a sí mismo como “una institución académica líder mundial, con una destacada historia y tradición en educación, enseñanza e investigación”.
Aunque la historia empieza un poco antes de conocerse allí: fue a finales de 1934 o principios de 1935, cuando el profesor William Dean visitó la escuela de nuestro primer protagonista, Arthur Stone, y en su charla afirmó que el problema de demostrar que un cuadrado no podía ser diseccionado en un número finito de cuadrados distintos (conocido como conjetura de Lusin) estaba aún sin resolver.
Se conocían entonces los llamados rectángulos perfectamente cuadrados o «rectángulos perfectos», que son aquellos que se pueden dividir en cuadrados distintos, como el —casi cuadrado— de dimensiones 33 x 32 que se puede descomponer en nueve cuadrados de lados 1, 4, 7, 8, 9, 10, 14, 15 y 18, descubierto por el matemático polaco Zbigniew Moron en 1925. Él mismo probó que es imposible construir un rectángulo perfecto con menos de nueve cuadrados. Más adelante, el propio Stone consiguió una disección del rectángulo de dimensiones 177 x 176 en once cuadrados diferentes.
Ya en 1902, el matemático autodidacta y famoso creador de rompecabezas Henry Dudeney había publicado en la revista «The London Magazine» un puzle titulado “Lady Isabel’s Casket”, en el que proponía dividir un cuadrado de dimensiones 20 x 20 en varios cuadrados de distinto tamaño y un rectángulo estrechito de dimensiones 10 x 0,25. Recientemente se ha descubierto que la solución dada por Dudeney no es única.
Después de ingresar al Trinity College en 1935, y con las palabras de Dean resonando en su cabeza, Arthur Stone compartió el problema con sus recién estrenados colegas, los estudiantes de Matemáticas Leonard Brooks y Cedric Smith y el chico de Químicas, William Tutte, más tarde autoproclamados ‘Important Members’ de la asociación de estudiantes ‘ The Trinity Mathematical Society’.
Durante el periodo 1936-1938 trabajaron en la conjetura, a la que Tutte bautizó irónicamente como la cuadratura del cuadrado, y lograron resolver el problema. ¿Cómo? Resultó cierto lo que parecía imposible: sí existen cuadrados que se pueden dividir en cuadrados más pequeños, todos ellos de distinto tamaño. No hay mejor demostración que encontrar una solución, y los cuatro amigos encontraron un cuadrado que se podía descomponer en 69 cuadrados diferentes.
Poco duró su alegría, pues pronto se enteraron de que el matemático alemán Ronald Sprague se les había adelantado al lograr descomponer un cuadrado de lado 4205 en otros 55 cuadrados diferentes, con ayuda de los rectángulos de Moron.
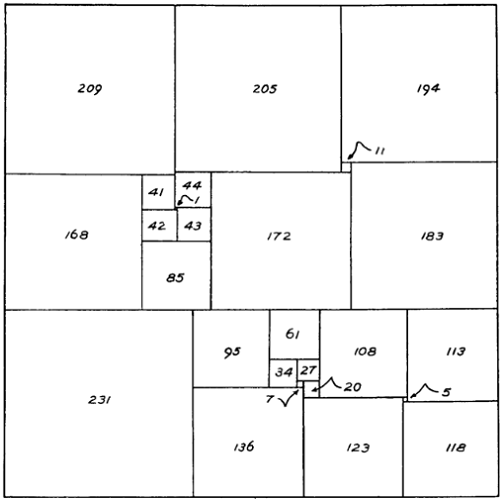
Ahora bien, a nuestros protagonistas se debe el estudio sistemático del problema, al reinterpretarlo en términos de circuitos eléctricos con resistencias variables (que llamaron diagramas de Smith), con lo que pudieron simplificar la búsqueda y lograr otras soluciones más pequeñas. De hecho, en 1940, los llamados ‘Cuatro de Trinity’ encontraron una solución considerablemente mejor: un cuadrado de lado 608 descompuesto en 26 cuadrados diferentes, gracias a esta preciosidad de fórmula:
En ese trabajo, estudiaron también el problema de ‘triangularizar triángulos’, es decir, descomponer un triángulo cualquiera en triángulos distintos pero todos equiláteros, utilizando la misma teoría de circuitos eléctricos asociados. No dan ninguna solución general pero indican que no existe ninguna descomposición de un triángulo equilátero en triángulos equiláteros distintos. Incluso se atreven con el problema tridimensional, de descomposición de un cubo en cubos distintos, pero lo finiquitan demostrando que no existe tal ‘cubo perfecto’.
Continúa leyendo en ABC CIENCIA
CURADAS | Tu compañía en información…